

Questions? Comments? Email me!
Osborn, John A. L., "Diminishing Opportunity in Amphography", editors: Gyorgy Darvas and Denes Nagy, Symmetry: Culture and Science, Volume 6, Number 3, pp. 418-421, 1995.
DIMINISHING OPPORTUNITY IN AMPHOGRAPHY
John A. L. Osborn
250 Donegal Way
Martinez CA, 94553, U.S.A.
E-mail: jalosborn@gmail.com
I propose that both the geometric means and the recognizable
zoomorphs, or animal shapes, which are essential to amphography are
limited in number or in quality, and that each figurative tiling which
is devised diminishes the number and the richness of opportunities for
future amphographers. Keenly felt ethical restrictions also affect
opportunities.
[Amphography is the art of figurative tiles and their tilings. The word derives from the fact that both (amph-) sides of the line are used to draw (graph-) an image.]
The ethical restrictions.
M. C. Escher was the first amphographer of significance. One of his
better-known works is The Horseman, of 1946. By devising this tile,
which is based on a kite-shaped quadrilateral and tiles the plane in
conjunction with its mirror image, Escher foreclosed forever the
possibility of any subsequent artist employing this user-friendly
geometry for the amphographic depiction of any even remotely related
subject matter without incurring the epithet "imitator", or
"derivative", or even "plagiarist." Much the same can be said about each
of his other 130 or so tilings.
There is justice in this. A figurative tiling that represents an
original combination of a particular zoomorphic type and a particular
geometric means is truly an invention. It will have about it that
quality of being the embodiment of an intellectual concept around which
the requirements for patentability seem to circle, but never
touch. A figurative tiling is a thing disciplined by the requirement of
functionality. In another category entirely, and I think rightly so, is
the superficial novelty which is all that is required for the
copyrightability of other works of art. There will, for instance, be
millions of original Madonna paintings, or horse prints, or dog
drawings. Thousands upon thousands of these will share a large number of
similarities. Nevertheless a few differences here and there will save
almost all of them from ethical opprobrium, for they exist in a far
freer and larger artistic universe than that of amphography.
Even an amphographic winged camel, on the other hand, would be
labeled imitative were it based on the kite geometry of Escher's
"Horseman." This is rightly so. One feels instinctively that the
inventive concept is being infringed.
The geometry, though, is seductively user-friendly: With it I've done
Pegasuses, Unicorns, Lady Godivas, drawn-bow Centaurs, and, (I blush to
admit), Winged Camels.
The limited number and quality of recognizable zoomorphs and geometric means.
An example of a different type of foreclosure may be my regular-hexagon based set of eight different beetle shapes. These are examples of a type of tile which I call variably assemblable figurative tiles. Ten subsets of the eight beetle shapes will tile the plane, some in more than one way, and eight of the subsets will tile in infinite numbers of different ways. I have derived other sets of shapes out of this geometry but, aside from minor variations on the beetle shapes, the geometry has yielded only poor of far-fetched zoomorphs. I believe that other good possibilities for variably assemblable figurative tiles simply do not exist in this geometry.
Here are the eight beetles: (Fig. 1)

This same sort of foreclosure occurs to a significant degree every
time an amphographer devises a figurative tiling. I, (among others, I'm
sure), have suspected that whenever M. C. Escher investigated the
possibilities of a fresh geometry, he liked to count coup on it by using
it for a lizard tiling. He did so many of them! Now, it is hard to do a
lizard tile, at least one involving the dorsal or "most significant"
aspect, without infringing M.C.E. Not only in this instance, but with
every figurative tiling devised, the good tiling possibilities tend
to get used up, and used up first. This is only a tendency, and there
may always be examples of striking originality which seem to contravene
it. An example in this case might be my variably assemblable sets of
lizard shapes and bat shapes. (See Figs.2 and 15)
Here are some of them: (Fig. 2 ) (Fig. 3 )
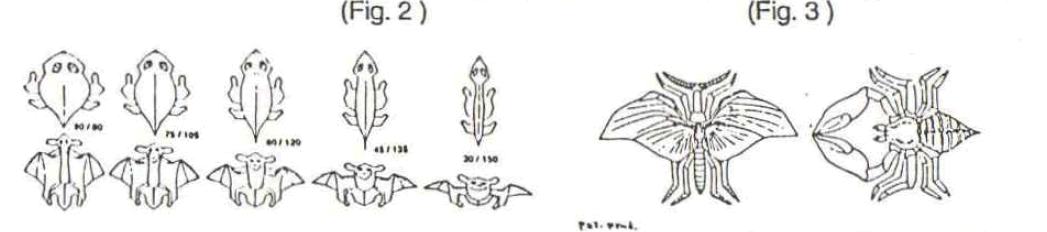
But again, by devising these bat and lizard sets, I may have largely foreclosed opportunity for variably assemblable zoomorphic figurative tilings using the two-figure/ variable rhombus geometry. I have also devised, using a 60 degree/120 degree rhombus only, a variably tiling arachnoid/insectoid set of tiles, (See Fig.3 above), but with that the richest possibilities inherent in this geometry are, I think, gone. Or is this a failure of my imagination?
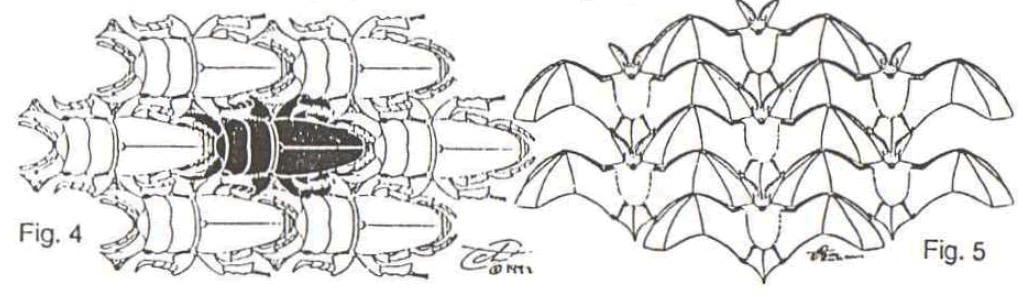
Among regularly repeating or periodic figurative tilings, possibilities for using the most significant aspect, (or what I sometimes call the roadkill aspect), are limited in number, and are being used up. Will anyone ever be able to do a simple beetle tiling, or bat tiling, or girl tiling, or turtle tiling, or moth tiling, or bug tiling with these geometries without "infringing" my work? See Figs. 4, 5, 6, 7, 8, and 9 respectively.

I don't know, but I think it will not be easy to do so. How many distinct and fully recognizable zoomorphic outlines are there for people in general or for persons of our western culture? Because we have never before thought of listing them, the number at first seems sure to be enormous. But really it is limited,--perhaps quite limited. There is, however, more room for 'creativity' once we leave the glyphic realm of "most significant aspect". Surely there may be other and quite dissimilar fish possibilities in the geometry I've used. See Fig.10.
But this realm of less significant aspects can rather quickly degenerate into one where the recognizability of the tile outline depends more and more heavily on clues gleaned from the internal drawing. I just recently devised the following outline, (Fig. 11), which only incidentally is composed entirely of straight lines.
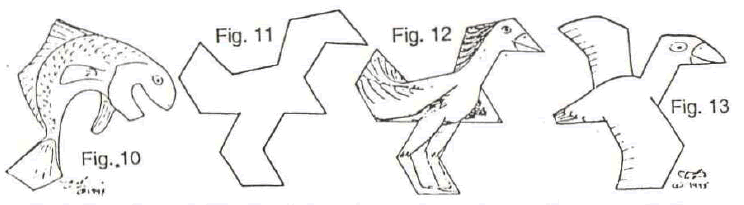
It might well be said that it utterly lacks amphographic quality. Yet with the benefit of a little internal drawing it becomes recognizable as some sort of roadrunner-like bird. ( Fig. 12) It is a variant on the geometry of the flying bird I've entitled "The Ozbird Tile," (Fig. 13), which is an equilateral-triangle based variably assemblable tile.
In my work, the most extreme example of a tile unrecognizable by its outline alone would, I think, be the Daruma in my "Birth of Zen". ( Fig.14) My only excuse is the extreme difficulty of the geometry in getting it to do what I wanted: use the Penrose rhombuses to pun on the philosophy of mind.
At some point close to my Daruma one enters Topffer's realm or the realm of Mr. Potato Head, something that I do not, (usually), care to do. "Figurative" no longer applies to these outlines. Hence the realm of "less significant aspects" too, is limited.
I believe that geometries amenable to use in amphography, while fairly numerous, are limited in number.
So we have ethical limitations, zoomorphic limitations, and geometric limitations.
This would seem to make amphography a severely limited universe. Perhaps the dynamics work something like this: If M. C. Escher used up half of the good possibilities, and then I used up half of the remainder, my successor may use half of what I leave, or a mere 1/8 of what lay open to Escher's exploration back in 1936 or 1937.
No, I do not think there need ever be a last figurative tiling of significant quality, but the possibilities for originality are rapidly becoming impoverished. If you want to do nice work in this field, hurry and join me. Sometimes I feel like the lone despoiler of a limited resource.
In this paper I have tried to be provocative, and I sincerely hope someone can show me to be wrong.
